|
|
Co-Ordinate Geometry - Quant/Math - CAT 2013
Question 4 the day:
May 8, 2002
- A and B are two points with the co-ordinates (-2, 0) and (0, 5). What is the length of the diagonal AC if AB form one of the sides of the square ABCD?
| (1) | 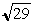 units units | | (2) | 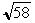 units units | | (3) | 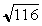 units units | | (4) | 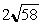 units units |
Correct Answer - (2)
Solution
Co-ordinate geometry is an important topic within geometry where one or two questions typically appear in CAT and other MBA entrance examinations in the Math section. The problems typically asked will involve one of the following types within co-ordinate geometry.
1. Reflection (or image) of a point P in a line (could be the co-ordinate axes themselves) and finding out the co-ordinates of the image P`.
2. Finding the length of a line given its co-ordinates. These problems could also include determining the type of polygon that will be formed by joining the co-ordinates. e.g. given the vertices of a polygon, determining if it is a square or a rectangle etc.
3. The ratio at which two lines intersect each other given their co-ordinates.
4. Finding out missing values in the equation of lines, given either that the lines in consideration are parallel to each other or are perpendicular to each other.
In today’s problem, we are given the co-ordinates of A and B. From this, we will be able to find the length of the line AB and hence one of the sides of the square ABCD.
If (x1, y1) and (x2, y2) are the co-ordinates of two point A and B, then the length of the line AB is given by 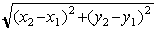 units. units.
In this case A (-2, 0) and B (0, 5) are the co-ordinates. Hence the length of the line = 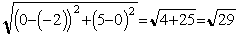 units. units.
The side of the square ABCD, therefore, is 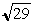 units. If ‘a’ is the length of a side of a square, then the length of diagonals of the square is given by units. If ‘a’ is the length of a side of a square, then the length of diagonals of the square is given by  .a. If ABCD is a square, then ABC and ACD will be two equal right angled triangles with AB = BC = CD = DA = ‘a’. The diagonal AC or BD are the hypotenuse of the respective right angled triangles whose length is given by Pythagorean theorem - (hyp)2 = (base)2 + (height)2. .a. If ABCD is a square, then ABC and ACD will be two equal right angled triangles with AB = BC = CD = DA = ‘a’. The diagonal AC or BD are the hypotenuse of the respective right angled triangles whose length is given by Pythagorean theorem - (hyp)2 = (base)2 + (height)2.
In this problem as the length of the side of the square is 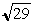 , the length of the diagonal AC = , the length of the diagonal AC =  units. units.
|
|
|
|



